Bezier Splines Simulator

En el análisis numérico se pueden encontrar las curvas de Bézier en el capítulo "curvas modeladas de forma paramétrica" ​​antes.

Esta aplicación está diseñada preferentemente para estudiantes de ciencias de la computación y matemáticas,

dibujo, que muestra a modo de ejemplo a las curvas de Bezier y ser capaz de modificar.

Ellos llevan el nombre de Pierre Bézier, un desarrollador con la empresa de automóviles francés Renault.

Esto se desarrolló a principios de 1960 con el propósito de diseños de carrocerías para el

diseño asistido por ordenador de los automóviles.

Ya unos años antes e independientemente de Bezier Paul de Casteljau desarrollado los mismos procedimientos

en Citroen. A su pesar, no se le permitió publicar los avances y gráficos

por eso, lleva el nombre de Bezier.

las curvas de Bézier son una forma especial de las curvas polinómicas

y se determinan mediante un cierto número de puntos de control.

Para la descripción matemática de las curvas de Bézier y sus puntos de control

Usando el nombre del matemático Sergei N. Bernstein Bernstein polinomio.

Cabe mencionar que la curva no pasa por todos los puntos de control,

pero sólo se ve influido por ellos.

Bernstein polinomio no son adecuados para la representación gráfica de una curva de Bezier,

debido a que su cálculo es demasiado tiempo. En su lugar, obtener en esta aplicación el

De Casteljau algoritmo utilizado. Determina las coordenadas de una

punto de la curva por la división sucesiva del polígono de control.

En resumen, se puede decir que las curvas de Bezier históricamente

modelo significativo para la representación de las curvas de forma libre y áreas.

Su cálculo se puede hacer rápidamente y fácilmente en los lenguajes de programación más comunes.

No en vano se encuentran en casi todas conferencia sobre "Computer Graphics"

tratamiento antes de este hilo.

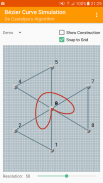
Con la ayuda de esta aplicación se puede llevar a cabo la representación de una curva de Bezier interactiva.

La aplicación es compatible con tres modos:

Introducción de bases

Los que se desplazan los puntos de apoyo individuales

Eliminación de bases individuales

Con la entrada de menú "Borrar", todo el contenido de la tela se pueden eliminar.

La resolución de la curva de Bezier (el número de puntos de la curva calculado)

se puede configurar con una barra deslizante en la parte inferior.

Una característica especial es la casilla de verificación "Mostrar la construcción". Para el funcionamiento del algoritmo

para demostrar de Casteljau, en este modo de visualización para la construcción

además, los puntos calculados actuales apuntan Bezier de esquema Casteljau indicados.

Como esto sólo es posible para un parámetro determinado t en el intervalo [0,1],

hay en la parte inferior de una segunda barra de cambio para este parámetro.

Las siguientes capturas de pantalla se pueden encontrar en el funcionamiento básico de la aplicación.

Versión 1.1 Nuevas Características / Nuevas Funcionalidades:

La aplicación es compatible con los idiomas

Alemán e Inglés - Soporte para dos idiomas alemán y se presentó Inglés.

La resolución de las estrías en los dispositivos con diferente resolución ha sido mejorada / se proporcionan mejoras y correcciones de errores Gemäß a la resolución del dispositivo.

Las mejoras en la documentación en línea de documentación / en línea añadió.

Ancho de línea regulable / Stroke Ancho ajuste siempre.

Versión 2.0 Nuevas características / Nuevas Funcionalidades:

El dibujo de curvas de Bezier puede ser apoyado por las líneas de división ahora / Dibujo de splines de Bezier ahora puede ser el apoyo de una vista 'snap-to-grid'.

Versión 3.0 Nuevas características / Nuevas Funcionalidades:

Con los elementos de menú "Guardar" y "carga" la curva de selección actual se almacena en los SharedPreferences la aplicación o restaurado. La aplicación se amplió por una llamada "consola de Bezier" (representación textual de los puntos de control).

El spline actual ahora se puede almacenar en las preferencias comunes de la aplicación. Más aún más un "Bezier consola" (vista textual de todos los puntos de control) se ha proporcionado.

Divertirse! - Have Fun!